sackur tetrode equation

Associative of partition function

$\mathcal Z = \sum_\alpha e^{-\beta E_\alpha} = \sum_i\sum_j e^{-\beta(E^{(a)}_i + E^{(b)}_j)}$

$= (e^{-\beta E^{(a)}_1} + e^{-\beta E^{(a)}_2} + \cdots)(e^{-\beta E^{(b)}_1} + e^{-\beta E^{(b)}_2} + \cdots) = \mathcal Z_a \cdot \mathcal Z_b$

Partion function of ideal gas

$E = \frac{1}{2} m v^2$

$\mathcal Z = \sum_\alpha e^{-\beta\frac{1}{2}mv^2_\alpha}\;\to\; \int^\infty_0 e^{-\beta frac{1}{2}mv^2}g(v)\,dv$

$g(v)$ is density of states

Quantumn magic

Infinte square wall

$\psi_n = \sqrt{\frac{2}{L}} \sin(kx), \quad (k=\frac{n\pi}{L})$

$\psi(x, y, z) = \psi_n(x)\psi_n(y)\psi_n(z) = \sqrt{\frac{2}{L}} \sin(k_x x)\sqrt{\frac{2}{L}} \sin(k_y y)\sqrt{\frac{2}{L}} \sin(k_z z)$

$=\frac{2}{L}^{3/2} \sin(k_x x) \sin(k_y y)\sin(k_z z)$

because expectation energy is

$\langle E\rangle= \frac{\hbar^2}{2m}\frac{n^2\pi^2}{L^2}$

in case of 3-D space,

$\langle E\rangle= \frac{\hbar^2}{2m}(\frac{n_x^2\pi^2}{L_x^2}+\frac{n_y^2\pi^2}{L_y^2}+\frac{n_z^2\pi^2}{L_z^2})$

$=\frac{\hbar^2}{2m}(k^2_x+k^2_y+k^2_z) = \frac{\hbar^2}{2m}\vec k^2$

$k_i = \frac{n_i\pi}{L_i}, \quad i = x, y, z$

$\vec k^2 = 2m \frac{\langle E \rangle}{\hbar^2}$

$\mathcal Z = \sum_\alpha e^{-\beta E} = \sum e^{-\beta \frac{\hbar^2}{2m}\vec k^2}$

Density of state

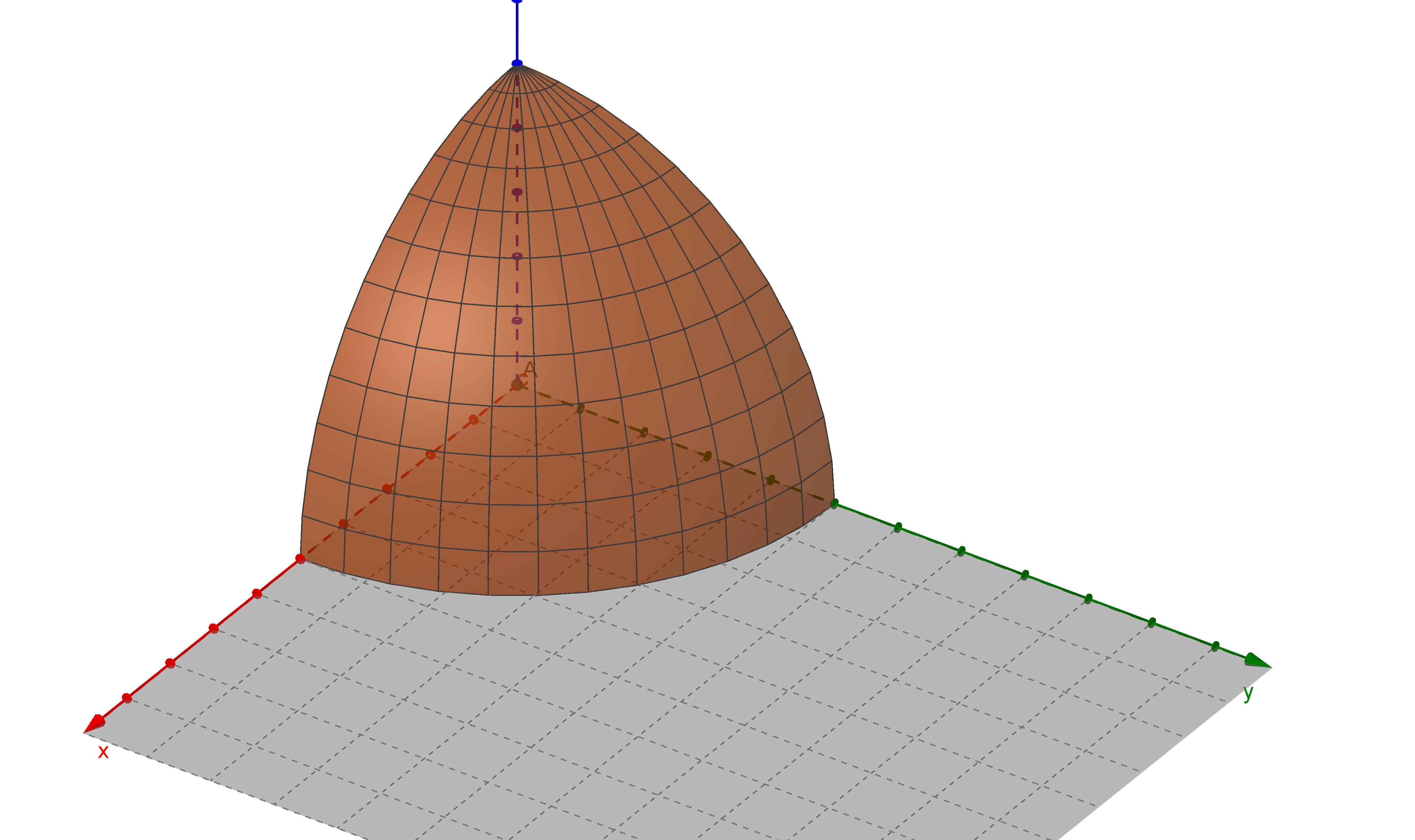
surface: $\frac{1}{8}(4\pi k^2)$

volume: surface $\times dk$

density of state:$\frac{\text{volume in k-space of one of a shell }}{\text{volume k-space occupied per allowed state}}$

$= \frac{\text{volume}}{(\frac{\pi}{L})^3} = \frac{k^2L^3}{2\pi^2}dk = \frac{k^2V}{2\pi^2}dk = g(k),\quad \text{number of state in }(k,\, k+dk)$

Thermal wavelength

$\mathcal Z = \int_0^\infty e^{-\beta \frac{\hbar^2}{2m}\vec k^2}\frac{k^2V}{2\pi^2}dk = \frac{V}{8\pi^2}(\frac{8m^3\pi}{\beta^3\hbar^6})^{\frac{1}{2}}$

$= \frac{V}{\hbar^3}(\frac{mkT}{2\pi})^{\frac{3}{2}}, \quad \beta=\frac{1}{kT}$

$=V \cdot n_Q,\quad (n_Q^{-1/3} = \frac{\hbar}{\sqrt{2\pi mkT}},\quad [m])$

$n_Q$ is quantum concentration.

the de-brogil wavelenth is $\lambda = \frac{\hbar}{p}$, we set $\sqrt{2\pi mkT}$ be average thermal momentum.

$\lambda_{th} = \frac{\hbar}{\sqrt{2\pi mkT}},\quad \text {thermal wave length}$

Indistinguishable

U(internal energy), F(helmholzt), S(entropy) Partition function

$U = -\frac{d}{d\beta}\ln(\mathcal Z_n)$, $F=-k_bT\ln(\mathcal Z)$, $S=\frac{U-F}{T}$

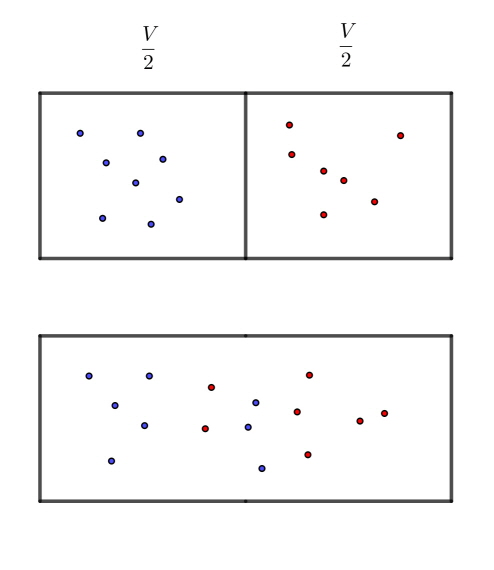
Gibb's paradox

The partition function of N free particles is

$Z_n = Z^n = (\frac{V}{\hbar^3}(\frac{m}{2\pi \beta})^{\frac{3}{2}})^N==(V\cdot n_Q)^N$

$U = -N\frac{d}{d\beta} \ln(\frac{V}{\hbar^3}(\frac{m}{2\pi \beta})^{\frac{3}{2}})=N\frac{3}{2}\frac{d\ln(2\pi \beta)}{d\beta}=N\frac{3kT}{2}$

$F=-kTNln(V\cdot n_Q)$

$S=N\frac{3k}{2} + kNln(V)$

$S_{before} = 2(\frac{N}{2}\frac{3k}{2} + k\frac{N}{2}ln(\frac{V}{2}))$

$S_{after} = N\frac{3k}{2} + kNln(V))$

$S_{after} - S_{before} = kNln(V) - kNln(\frac{V}{2}) \neq 0$

Indistinguishability of the particles

$Z_n = \frac{Z_1^n}{N!}$

$Z_n = \frac{Z^n}{N!} = \frac{1}{N!}(\frac{V}{\hbar^3}(\frac{m}{2\pi \beta})^{\frac{3}{2}})^N=\frac{(V\cdot n_Q)^N}{N!}$

$U = -N\frac{d}{d\beta} \ln(\frac{1}{N!}\frac{V}{\hbar^3}(\frac{m}{2\pi \beta})^{\frac{3}{2}})=N\frac{3}{2}\frac{d\ln(2\pi \beta)}{d\beta}=N\frac{3kT}{2}$

$F=-kT(Nln(V\cdot n_Q)-\ln(N!))=-kT(Nln(V\cdot n_Q)-N\ln(N) + N)=-kTN\ln(\frac{V\cdot n_Q\cdot e}{N})$

$S=kN(\frac{3}{2} + \ln(\frac{V\cdot n_Q\cdot e}{N}))=kN\ln(\frac{V\cdot n_Q\cdot e^{5/2}}{N}),\quad \text{Sackur-tetrode equation}$

$S_{before} = 2(k\frac{N}{2}\ln(\frac{V\cdot n_Q\cdot e^{5/2}}{N}))$

$S_{after} = kN\ln(\frac{V\cdot n_Q\cdot e^{5/2}}{N}))$

$S_{after} - S_{before} = 0$