Topology summary

• Topology summary
  • Continuous map
  • Homeomorphism
  • Space-filling curve
  • A metric function
  • Tietze extension theorem.
  • Compact spaces
    • Other defintion of a compactness in terms of closed subsets
    • Heine-Borel theorem
  • Connectedness
    • component
    • joinning poins by path
  • Homotopic map

Continuous map

Definition
A function $f:X \to Y$ is said to be continuous if for each open subset $V$ of $Y$, $f^{-1}(V)$ is an open set of $X$.

Let $X$, and $Y$ be topologies. The followings are equivalent

1. $f:X \to Y$ is continuous.
2. for every closed set $B$ of $Y$, $f^{-1}(B)$ is closed in $X$.
3. $f(\overline A) \subseteq \overline {f(A)}$ and $\overline {f^{-1}(B)} \subseteq f^{-1}(\overline B)$ for $A \subset X$, $B \subset Y$.
4. For each $x \in X$ and each neighborhood $V$ of $f(x)$, there is a neighborhood $U$ of $x$ such that $f(U) \subset V$
5. for a basis $B$ of $Y$, $f^{-1}(B)$ is open in $X$.

Homeomorphism

Let $X$ and $Y$ be topological spaces; let $f:X \to Y$ be a one-to-one, onto, continuous, and the inverse function is continuous, then $f$ is a Homeomorphism.
Let $S^n$ be a n-dimensional sphere, $p = (0,\,\ldots,\,0, 1)$ be the north pole. $h:S^n - \{p\} \to \mathbb R^n$be the Stereographic projection is defined.

Space-filling curve

Let $I=[0,1]$, there exists $f: I \to I\times I$ such that this map fill up the entire square $I^2$.

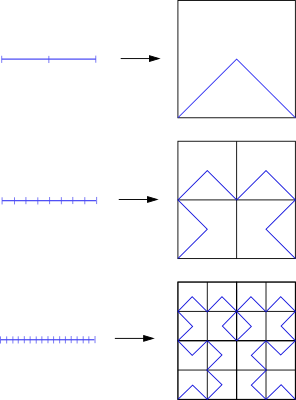
For $\displaystyle\lim_{m \to \infty} f_m \to f$ and $d:(I^2, I^2) \to R$ is distance, $\displaystyle\lim_{n \to \infty}d(f_n,f) \to 0$. and then since $f_n$ is a continuous, $f$ is continuous.

A metric function

1. $d: X \times X \to \mathbb R$
2. $d(x,y) \ge 0$, equality holds iff $x=y$
3. $d(x,y) = d(y,x)$
4. $d(x,y) + d(z,y) \ge d(x,y)$

a set with a metric is called a metric space.

a distance between two functions is $d(f,g) = \displaystyle\sup_{t \in [0,1]}|f(t) - g(t)|$

if $A$ is a subset of $X$, the real-valued function $d(x,A)$ is defined to be the infimum of $d(x,A)$ where $a \in A$ and is continuous.

Tietze extension theorem.

Any real valued continuous function on a closed subset of a metric space may be extended to a real-valued continuous function on the whole space.

Compact spaces

Definition
Let $\mathcal A$ be a collection of open subsets of space $X$. $\mathcal A$ is called an open cover of $X$ such that $\bigcup \mathcal A = X$. and $\mathcal A'$ is called a subcover of $\mathcal A$ if $\mathcal A'$ is a subcollection of $\mathcal A$ and $\bigcup \mathcal A' =X$.
A space $X$ is said to be compact, if all open cover of $X$ has a finite subcover.

Other defintion of a compactness in terms of closed subsets

• If $X$ is compact, for every collections $\mathcal C$ of closed sets $c_a$ with $\bigcap c_a = \emptyset$, $\mathcal C$ has a subcollections $\{C_1,\, \ldots,\,C_n\}$ such that $\bigcap_{i \to 1}^{n} C_i = \emptyset$.
• $X$ is compact. $\Rightarrow$ $\mathcal C$ is a collection of closed sets of $X$ such that for all finite subcollection $\{C_1,\,\ldots,\,C_n\}$, $\bigcap_{i \to 1}^{n} c_i \neq \emptyset$. then for every collection $\mathcal C$, $\bigcap_{a \in All} C_a \neq \emptyset$.

Heine-Borel theorem

A closed interval of the real line is compact.

Connectedness

Definition
A space $X$ is connectedness if when we write $X$ as union $A \cup B$ of two nonempysubsets, then $\bar A \cap B \neq \emptyset \text{ or } A \cap \bar B \neq \emptyset$. in other words, $X$ is not seperated by disjoint nonempty open subsets.

Examples

1. A indiscrete topology is a connected space.
2. The real line is a connected space.
3. A rational $\mathbb C$ is not a connected space.

component

a component of topology $X$ is a maximal connected subset of $X$. so if a space is not connected then it is seperated by any components.

joinning poins by path

Given $x, y \in A$, A path in the topological space $A$ is a continuous function $f:[a, b] \to A$ such that $f(a)=x$, $f(b)=y$. and A space $A$ is said to path connected if any two of its points can be joined by a path.

Examples

1. the continuous image of path-connected space is path-connected.
2. $S^n$(n sphere) is path-connected for $n > 0$.
3. the product of two path-connected space is path-connected.
4. any indiscrete space is path-connected.

Homotopic map

Definition
Let $X, Y$ be topological spaces.Let $f,g:X \to Y$ are continuous. $f$ is homotopic to $g$ if there exists $F:X \times [a, b] \to Y$ such that $F(x,0) = f(x)$ and $F(x,1)=g(x)$ for all points $x \in X$.
and this continuous map $F$ be called homotopy from $f$ to $g$ .