• • 6.Closed set and Limit points
    • Closed sets
    • Closure and Interior of a set
    • Hausdorff spaces

6.Closed set and Limit points

we treat notations of closed set, closure of set and limit point. These lead naturally to consideration of a certain axiom for topological spaces called the Hausdorff axiom.

Closed sets

A subset $A$ of a topological space $X$ is said to be closed if the set X−A is open.

ex1) the subset $[a,b]$ of R is closed because its complement

is open. similarly [a,+∞) is closed, because ints complement (−∞,a) is open. these facts justify our use of terms closed interval and closed ray. the subset $[a,b)$ of R is neither open nor closed.

ex2) In the plane $\mathbb R^2$, the set

${x \times y \, | \, x \ge 0 \; \text{and} \; y\ge 0 }$

is closed, because its complement is the union of the two sets

$(-\infty) \times \mathbb R \;\text{and}\; \mathbb R \times (-\infty,0)$

each of which is a product of open sets of and is open in $\mathbb R^2$.

ex3) In the finite complement topology on a set $X$, the closed sets consist of $X$ itself and all finite subsets of $X$.

ex4) In the discrete topology on the set $X$, every set is open; it follows that every set is closed as well.

ex5) consider the following subset of the real line

$Y=[0,1]\cup(2,3)$

in the subspace topology. In this space, the set $[0,1]$ is open. similarly $(2,3)$ is open as a subset of $Y$; it's even open in $\mathbb R$. since $[0,1]$ and $(2,3)$ are complements in $Y$ of each other, we conclude that both are closed as subset of $Y$.

Theorem 17.1 Let $X$ be a topological spaces. then the following conditions hold

1. $X$ and $\phi$ are closed
2. Arbitrary intersections of closed sets are closed
3. Finite unions of closed sets are closed

proof.

1. $\phi$ and $X$ are closed because they are the complements of the open sets $X$ and $\phi$, respectively.

2. Given a collection of closed sets $\{A_\alpha\}_{\alpha \in j}$, Applying DeMorgan's law
   $X - \bigcap_{\alpha \in j}\{A_\alpha\}=\bigcup_{\alpha \in j}(X-A)$
   since the sets X−A_α are open by definition, the right side represents an arbitrary union of open sets, and is open. therefore $\cap A_\alpha$is closed.

3. similiarly if $A_i$ is closed for i=1, ⋯,n, consider the equation
   $X-\bigcup_{i=1}^{n}A_i= \bigcap_{i=1}^n(x-A_i)$
   The set on the right side is a finite intersection of open sets and is open. hence $\cup A_i$ is closed.

If $Y$ is a subspace of $X$, we say that a set $A$ is closed in $Y$ if $A$ is a subset of $Y$ and $A$ is closed in the subspace topology of $Y$.

Theorem 17.2 Let $Y$ be a subspace of $X$. then a set $A$ is closed in $Y$ if and only if it equals the intersection of a closed set of $X$ with $Y$.

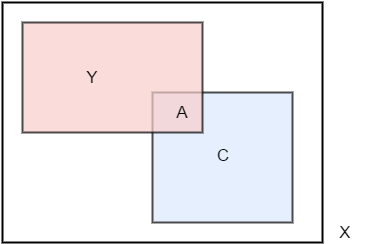
proof. Assume that $A=C \cup Y$, where $C$ is closed in $X$ (see Fig 17.1) then X−C is open in $X$, so that $(X-C) \cup Y$ is open in $Y$, by definition of the subspace topology, but $(X-C) \cap Y=(X \cap Y)-(C \cap Y)=Y-A$. hence $Y-A$ is open in $Y$. so that $A$ is closed in $Y$. conversely, assume that $A$ is closed in $Y$(Fig 17.2) then Y−A is open in Y, so by definition it equals the intersection of an open set U of X with Y. the set X−U is closed in X, and

$Y-A=U\cap Y$

$A=Y-(U\cap Y)=(X\cap Y)-(U\cap Y)=(X-U)\cap Y$

so that $A$ equals the intersection of a closed set of $X$ with $Y$, as desired.

Theorem 17.3 Let $Y$ be a subspace of $X$. If $A$ is closed in $Y$ and $Y$ is closed in $X$, then A is closed in $X$.

proof. since $A$ is closed in $Y$, by thm 17.2, $A=C\cup Y$, where $C$ is closed in $X$. so that A is closed in $X$. because $Y$ is closed in $X$, by closed condition 2.

Closure and Interior of a set

Given a subset $A$ of a topological space $X$, the interior of $A$ is defined as the unions of all open set contained in $A$. and the closure of $A$ is defined as the intersections of all closed set containing $A$. The interior of $A$ is denoted by $Int\, A$ and the closure of $A$ is denoted by $ClA$ by $\overline A$. obvisously $IntA$ is an open set and $\overline A$ is a closed set; furthermore,

$IntA\subset A \subset \overline A$

if $A$ is open, $A=Int\,A$; while $A$ is closed, $A=\overline A$.

Theorem 17.4 Let $Y$ be a subspace of $X$; Let $A$ be a subset of $Y$; Let $\overline A$ denoted by a closure of $A$ in $X$. then a closure of $A$ in $Y$ equals $\overline A \cap Y$.

proof. Let $\overline B$ denoted by a closure of $A$ in $Y$. the set $\overline A$ is closed in $X$. so $\overline A \cap Y$ is closed in $Y$ by Thm 17.2. since $\overline A \cap Y$ contains $A$, and since by definition, $\overline B$ equals the intersections of all closed set containing $A$, we must have $\overline B \subset (\overline A \cap Y)$.
on the other hand, we know that $\overline B$ is closed in $Y$. hence by thm 17.2, $\overline B = C \cap Y$ for some set $C$ is closed in $X$. then $C$ is a closed set of $X$ containing $A$; because $\overline A$ is the intersections of all such closed sets we conclude $\overline A \subset C$ then $(\overline A \cap Y ) \subset ( C \cap Y ) = B$.

The definition of the closure doesn't give us a convenient way for finding the closures of a specific set.
First let us introduce some convenient terminology. we shall say that a set $A$ intersects a set $B$ in the intersection $A\cap B$ is not empty.

Theorem 17.5 Let $A$ be a subset of the topoloical space $X$.
(a) then $x \in \overline A$ if and only if every open set $U$ containing $x$ intersects $A$.
(b) supposing the topology of $X$ is given $\mathcal B$ by a basis, then $x \in \overline A$ if and only if every basis element $B$ containing $x$ intersects $A$.

proof.consider the statement in (a), It's a statement form $P \Leftrightarrow Q$. Let us transform each implication to its contrapositive, thereby obtaining the logically equivalent statement $\neg P \Leftrightarrow \neg Q$ written out, it's following.
$x \notin \overline A$ $\Leftrightarrow$ there exists an open set $U$ containing $x$ that doesn't intersect $A$.
In this form, our theorem is easy to prove.
If $x$ is not in $\overline A$, the set $U = X - \overline A$ is an open set containg $x$ that doesn't intersect $A$.
conversely, if there exists an open set $U$ containing $x$ which doesn't intersect $A$, then $X-U$ is a closed set containing $A$. by definition of the closure $\overline A$, the set $X-U$ must contain $A$; therefore $x$ cannot be in $\overline A$.
Statement (b) follows readily, If every open set containing $x$ intersects $A$, so does every basis element containing $x$, because $B$ is open. conversely if every basis element containing $x$ intersects $A$, so does every open set $V$ containing $x$ because $V$ contains a basis element that contains $x$.

we shorten the statement "$U$ is an open set containing $x$" to the phrase
    "$U$ is a neighborhood of $x$"
using this terminology, one can write the first half of the preceding theorem as follows.

If $A$ is a subset of topological space $X$, then $x \in \overline A$ if and only iff every neighborhood of $x$ intersects $A$.

Example Let $X$ be the real line $\mathbb R$. If $A=(0,1]$ for every neighborhood of 0 intersects $A$, while every point outside $[0,1]$ has a neighborhood disjoint from $A$. similar arguments apply to the following subset of $X$:
If $B=\{1/n\,|\,n \in \mathbb Z_+\}$, then $\overline B = \{0\}\cup B$. If $C=\{0\}\cup (1,2)$ then $\overline C = \{0\} \cup [1,2]$. If $\mathbb Q$ is the set of ational numbers then $\mathbb {\overline Q} = \mathbb R$, $\overline {\mathbb Z}_+ = \mathbb Z_+$. if $\mathbb R_+$ is the set of positive reals, then the closure of $\mathbb R_+$ is $\mathbb R_+ \cup \{0\}$.

Example Consider the subspace $Y=(0,1]$ of the real line $\mathbb R$. the set $A=(0, \frac{1}{2})$ is a subset of $Y$; its closure in $\mathbb R$ is the set $[0,\frac{1}{2}]$ and its closure in $Y$ is the set $[0,\frac{1}{2}]\cap Y = (0,\frac{1}{2}]$.

Limit Points

If $A$ is a subset of the topological space $X$ and if $x$ is a point of $X$, we say that $x$ is a limit point of $A$ if every neighborhood of $x$ intersects $A$ in some point other than $x$ itself. say differently,
$x$ is a limit point of $A$ if it belongs to the closure of $A-\{x\}$.

Example Consider the real line in $\mathbb R$, If $A=(0,1]$, then the point 0 is a limit point of $A$ and so is the point $\frac{1}{2}$ In fact every point of the interval $[0,1]$ is a limit point of $A$.
    If $B=\{ \frac{1}{n} \,|\, n \in \mathbb Z_+\}$, then 0 is the only limit point of $B$. if $C=\{0\} \cup (1,2)$ then the limit point of $C$ are the points of the interval $[1,2]$. a limit point of $\mathbb Q$ is every point of $\mathbb R$. a limit point of $\mathbb Z_+$ is no point of $\mathbb R$. a limit point of $\mathbb R_+$ is a point of $\{0\} \cup \mathbb R_+$.

Theorem 17.6 Let $A$ be a subset of the topological space $X$; Let $A'$ be the set of all limit points of $A$ then $\overline A = A \cup A'$.

proof. If $x$ is in $A'$, every neighborhood of $x$ intersects $A$. therefore, by thm 17.5 $x$ belongs to $\overline A$ hence $A' \subset \overline A$, since by definition $A \subset \overline A$, $A\cup A' \subset \overline A$.
To demonstrate the reverse inclusion, we let $x$ be a point of $\overline A$ and show that $x \in A \subset A'$. if $x$ happens to lie in $A$, it is trivial that $x \in A \cup A'$; suppose that $x$ does not lie in $A$. since $x \in \overline A$, we know that every neighborhood $U$ of $x$ intersects $A$; because $x \notin A$, the set $U$ must intersect $A$ in a point from different from $x$; then $x$ is a limit point , $x \in A'$, so that $x \in A \cup A'$.

Corollary 17.7 A subset of a topological space is closed if and only if it contains all its limit points.

proof. the set $A$ is closed if and only if $A=\overline A$ and the latter holds if and only if $A'\subset A$.

Hausdorff spaces

Definition A topological space $X$ is called Hausdorff space if for each pair $x_1$, $x_2$ of distinct points of $X$, there exists neighborhood $U_1$ and $U_2$ of $x_1$, $x_2$, respectively, that are disjoint.

Theorem 17.8 Every finite point set in Hausdorff space $X$ is closed.

proof. It suffices to show that every one-point $\{x_0\}$ is closed. if $x$ of $X$ is different from $x_0$, then $x$ and $x_0$ has disjoint neighborhood $U$ and $V$, respectively. since $U$ does not intersect $\{x_0\}$, the point $x$ cannot belong to the closure of $\{x_0\}$. as a result, the closure of the $\{x_0\}$ is itself, so that it is closed.

The condition that finite point sets be closed is in fact weaker than Hausdorff condition. for example,the real line $\mathbb R$ in the finite complement topology is not a Hausdorff space, but it is a space in which finite sets are closed.
the condition that finite sets be closed has been given a name of tis own: its called $T_1$ axiom.

Theorem 17.9 Let $X$ be a space satisfying the $T_1$ axiom; Let $A$ be a subset of $X$. then the point $x$ is a limit point of $A$. if and only if every neighborhood of $x$ contains infinitely many points of $A$.

proof. If every neighborhood of $x$ intersects $A$ in infinitely many points, it intersects $A$ in some points other than $x$ itself so that $x$ is a limit point of $A$.
conversely, suppose that $x$ is a limit point of $A$, and suppose some neighborhood $U$ of x intersects $A$ in only finitely many points, then $U$ also intersects $A-\{x\}$ in finitely points; let $\{x_1,\, \ldots,\, x_n \}$ be the points of $U \cap (A-\{x\})$. the set $X-\{x_1,\, \ldots,\, x_n \}$ is open, since the finite point set $\{x_1,\, \ldots,\, x_n \}$ is closed.

$U \cap (X-\{x_1,\,\ldots,\, x_m\})$

is a neighborhood of $x$ that intersects $A$. thist contradicts assumption that $x$ is a limit point of $A$.

Theorem 17.10 If $X$ is a hausdorff space, then a sequence of points of $X$ converges to at most one point of $X$.

proof. Suppose that $x_n$ is a sequence of points that converges to $x$. if $y \neq x$, let $U$ and $V$ be disjoint neighborhood of $x$ and $y$, respectively. since $U$ contains $x_n$ for all but finitley many values of n, the set $V$ cannot. therefore, $x_n$ cannot converge to $y$.

Definition If the sequence $x_n$ of points of the Hausdorff space $X$ converges to the point $x$ of $X$, we often write $x_n \to x$, and we say that is the limit of the sequence $x_n$.

Theorem 17.11 (1)Every simply ordered set is a Hausdorff space in the order topology. (2)the product of two Hausdorff space is a Hausdorff space. (3)A subspace of a Hausdorff space is a Hausdorff space.

proof. (1) If $x_1 < x_2$, $x_1\, x_2$ is points of the ordered space $X$. $(-\infty,\,x1),\,(x_2,\,\infty)$ is elements of the ordered topology, that are disjoint.
(2) Let $X$ and $Y$ be a Hausdorff spaces. there exists $U_1$ and $U_2$ that contains $x_1$ and $x_2$, respectively. which are disjoint the the topology of $X$. similiary there exists $V_1$ and $V_2$ in the space $Y$. $x_1 \times y_1$, $x_2 \times y_2$ belong to $U_1\times V_1$ and $U_2 \times V_2$, respectively. $U_1\times V_1$ and $U_2 \times V_2$ are disjoint.
(3) let $A$ be a subset of the Hausdorff space $X$. there exists $U_1$ and $U_2$, which are open and disjoint, that contains $x_1$ and $x_2$, respectively. $x_1$ is different than $x_2$. and $A$ contains $x_1$ and $x_2$. then $A\cap U_1$ and $A \cap U_2$ is open in the subspace topology of $A$, that are disjoint.